NN-Tool
Prognose * Simulation * Optimierung
|
Bärmann
Software
|
|
Home Modellierung
Simulation Optimierung
Software Technik
Kunden Downloads
Kontakt Impressum |
Prozessmodellierung
und Rezepturoptimierung
1. Einführung
Aktuelle wirtschaftliche, rechtliche und ökologische Rahmenbedingungen erfordern eine ständige Weiterentwicklung und Optimierung chemischer Prozesse. Um im derzeitigen Wettbewerbsumfeld bestehen zu können, ist unter anderem eine gleichbleibend hohe bzw. ständig verbesserte Produktqualität erforderlich. Auf der Basis eines hinreichend genauen Anlagenmodells können optimale Betriebspunkte sowie verbesserte Rezepturen berechnet werden. Zur Entwicklung eines entsprechenden Modells können prinzipiell zwei Wege eingeschlagen werden:
Beide Methoden weisen Vor- und Nachteile auf. Die Entwicklung eines rigorosen Modells führt in der Regel zu einem tieferen Anlagenverständnis. Darüber hinaus besteht bei einem rigorosen Modell ggf. die Möglichkeit zur Extrapolation der Erkenntnisse auf neu zu errichtende Anlagen. Diesen Vorteilen steht jedoch eine Reihe von Nachteilen gegenüber. So sind für viele interessierende Größen entsprechende physikalische Beziehungen überhaupt nicht bekannt. Dies trifft insbesondere für (makroskopische) Qualitätsgrößen wie Viskosität, optische Eigenschaften, Schlagzähigkeit etc. zu. Darüber hinaus liegt die mit rigorosen Modellen erreichbare Modellierungsgenauigkeit in der Regel deutlich unter der Genauigkeit empirischer Modelle. Eine präzise Formulierung der Qualitätsgrößen eines Prozesses auf der Basis sämtlicher Einflussfaktoren (einige Dutzend bis mehrere Hundert) mit physikalischen Beziehungen erreichen zu wollen, erscheint aussichtslos. Eine Verbesserung der Betriebspunkte einer Anlage in der Größenordnung von einigen Prozent (alle darüberhinausgehenden Versprechungen sind eher unrealistisch), setzt ja eine Modellgenauigkeit voraus, die mindestens in dieser Größenordnung liegt. Ein weiterer wesentlicher Vorteil der Verwendung empirischer Modelle ist der relativ geringe Modellierungsaufwand. Ausgehend von Messdaten, die bei modernen Anlagen ohnehin anfallen, kann die Modellierung durch eine geeignete Software mehr oder weniger automatisch durchgeführt werden. Der Modellierungsaufwand liegt in der Größenordnung von einigen Manntagen. Als Standardverfahren zur Modellierung auch nichtlinearer Zusammenhänge haben sich neuronale Netze etabliert. Im Folgenden wird zunächst die Methodik vorgestellt und anschließend spezifische Aspekte der Anlagenoptimierung diskutiert. 2. Methode der
neuronalen Netze
Künstliche neuronale Netze (KNN) sind spezielle mathematische Modelle, die in besonderer Weise für Aufgaben des Anforderungstyps "Mustererkennung" geeignet sind. Dieser Begriff ist ganz allgemein zu verstehen, umfasst aber insbesondere das Erkennen von funktionalen Zusammenhängen zwischen physikalischen, chemischen, wirtschaftlichen etc. Größen. Durch diese Eigenschaften bilden künstliche neuronale Netze ein leistungsfähiges Instrument, um das in einer Vielzahl von Datenbanken bzw. Messdatenerfassungssystemen in Form von Anlagen- und Prozessmesswerten latent vorhandene Wissen über Verfahren, Prozesse, chemische Rezepturen etc. aufzudecken und für Anwendungen nutzbar zu machen. Insbesondere bieten KNNe die Möglichkeit auf der Basis von Messdaten aus der Anlagenhistorie ein Modell des zugrundeliegenden Prozesses zu generieren. Dabei werden keine a priori Annahmen über die Struktur der funktionalen Zusammenhänge zwischen verschiedenen Größen benötigt (im Gegensatz etwa zu linearen Regressionsansätzen mit nichtlinearen Ansatzfunktionen). Da die Automatisierung in der Industrie beständig zunimmt und somit für eine immer größere Zahl von Anlagen entsprechende Messdatenerfassungssysteme zur Verfügung stehen, kann davon ausgegangen werden, dass von dieser Möglichkeit in Zukunft zunehmend Gebrauch gemacht werden wird. Eine solcher Ansatz zeichnet sich gegenüber einer Modellierung auf der Basis physikalischer Gleichungen durch die folgenden Eigenschaften aus:
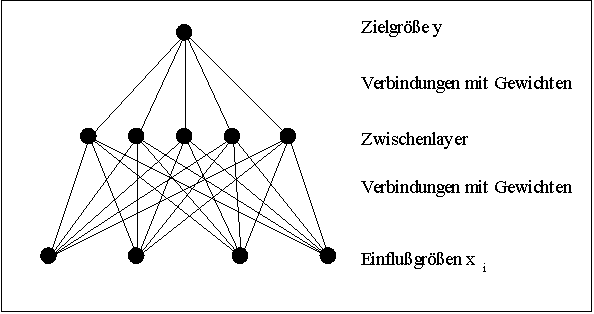
Künstliche neuronale Netze entstanden aus dem Versuch die Informationsverarbeitung in biologischen Systemen zu kopieren und technisch nutzbar zu machen. Ein neuronales Netz besteht aus einer Menge miteinander vernetzter Verarbeitungseinheiten, auch Neuronen, Prozessoren oder Knoten genannt. Ein Teil dieser Einheiten dient der Kommunikation mit externen Ein- und Ausgabequellen (Tastatur, Prozessleitsysteme etc.). Die in der Praxis am häufigsten verwendeten neuronalen Netze sind vom Typ der "feedforward networks", bei denen die Neuronen in Schichten (Layers) angeordnet sind. Jedes Neuron erhält Eingangswerte von allen Neuronen der vorhergehenden Schicht und gibt seinen Ausgangswert an alle Neuronen der nachfolgenden Schicht (Abb. 1).
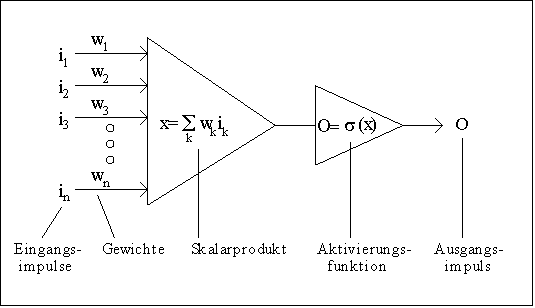
Abb. 1: Voll verbundenes Netz mit drei Schichten (Layers) Die Eingänge eines jeden Neurons sind mit "Gewichten" versehen. Innerhalb einer jeden Verarbeitungseinheit wird ein Skalarprodukt der Eingangswerte mit den Gewichten gebildet und auf den Ergebniswert eine Funktion, die sogenannte Aktivierungsfunktion, angewendet. Der entstehende Wert wird an die Neuronen der nachfolgenden Schicht weitergegeben (Abb. 2).
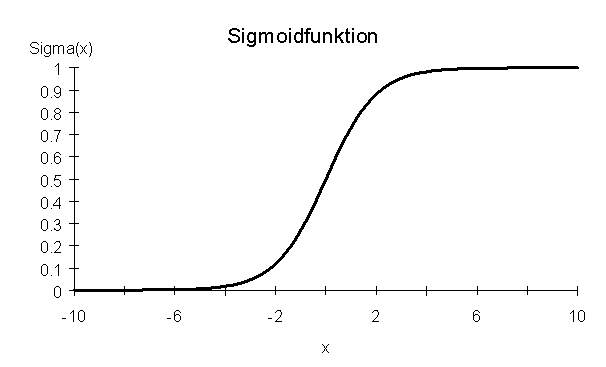
Abb. 2: Schema einer Verarbeitungseinheit im neuronalen Netz Die Neuronen der ersten Schicht (Inputlayer) bilden die Einflussgrößen xi, die Neuronen der letzten Schicht (Outputlayer) liefern die entsprechenden Funktionswerte. Als Aktivierungsfunktion hat sich eine sogenannte Sigmoidfunktion bewährt (Abb. 3).
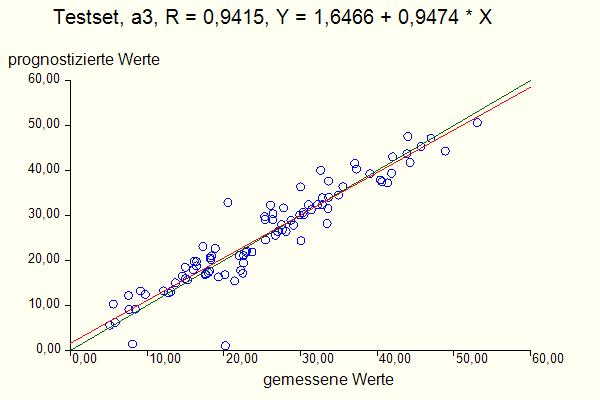
Abb. 3: Sigmoidfunktion Die Gewichte wi werden anhand von Beispieldatensätzen mittels eines numerischen Verfahrens an die konkrete Aufgabenstellung angepasst. Nach Abschluss dieser sogenannten "Lernphase" bildet das neuronale Netz ein in gewissem mathematischen Sinne optimales "Black-Box-Modell" des gesuchten funktionalen Zusammenhangs. Zur Beurteilung der Güte eines solchen Modells wird das Modell nun auf Beispieldatensätzen getestet, die nicht zur Erstellung des Modells herangezogen wurden (sogenannter Testset). Dabei wird der auf der Basis der Eingangsgrößen prognostizierte Wert einer Ausgangsgröße mit den vorgegebenen gemessenen Werten in einem sogenannten Scatterplot verglichen (Abb. 4). Bei exakter Prognose (d.h. wenn der prognostizierte Wert exakt mit dem gemessenen übereinstimmt) müssten die Punkte im Diagramm genau auf der Linie y = x (Winkelhalbierende) liegen und die Korrelation R würde den Wert 1 annehmen. Dies ist aber schon aufgrund der Messfehler bei realistischen Daten unmöglich. Je nach Qualität der Messdaten und Vollständigkeit der relevanten Einflussgrößen müssen Korrelationen oberhalb von 0,8 schon als zufriedenstellend angesehen werden.
Abb. 4 Scatterplot Aus der linearen Auftragung im Scatterplot darf nicht der Schluss gezogen werden, dass die Ausgangsgrößen linear von den Eingangsgrößen abhängen. Im Scatterplot werden die prognostizierten Ausgangsgrößen mit den gemessenen Ausgangsgrößen verglichen. Der Zusammenhang von Ausgangsgrößen und Eingangsgrößen kann auf der Basis des erstellten Modells in sogenannten Einflussplots untersucht werden (Abb. 5):
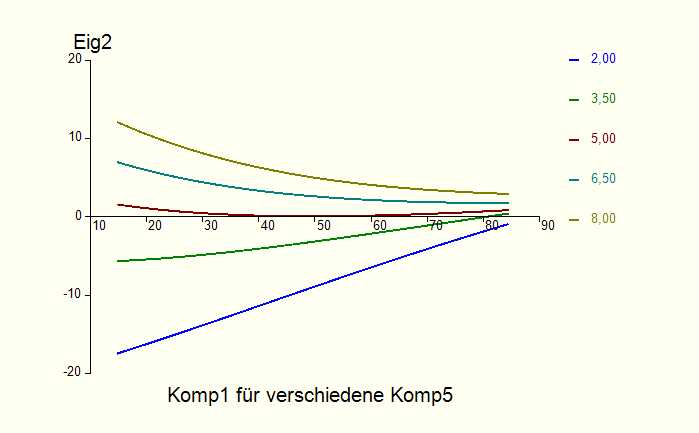
Abb. 5: Einfluss der Eingangsgrößen Komp1 und Komp5 auf die
Qualitätsgröße Eig2 Wie die Abbildung 5 zeigt, ist in diesem Beispiel der Einfluss der Messgröße Komp1 auf die Qualitätsgröße Eig2 nichtlinear und hängt darüber hinaus auch vom Wert der Messgröße Komp5 ab. Dies ist geradezu charakteristisch für allgemein nichtlineare Zusammenhänge. Das erstellte Modell kann nun u.a. zur Optimierung der Zielgrößen (z.B. bei der Bestimmung optimaler Betriebspunkte von Anlagen) herangezogen werden. Die Einsatzschwerpunkte neuronaler Netze in der Industrie liegen zum einen in der Modellierung von Verfahren und Anlagen. Typische Anwendungen sind Optimierungen von Betriebspunkten, Messdatenüberwachungen, online Fehlerdiagnosen und Anlagenregelungen. Den anderen Schwerpunkt bildet der Einsatz neuronaler Netze zur Auswertung und Optimierung von Versuchsreihen (Analyse von Rezeptur-Eigenschaftsbeziehungen, Prognose von Stoffeigenschaften).
3. Struktur und
Anwendungsbereich der neuronalen Netzsoftware NN-Tool
NN-Tool basiert ganz wesentlich auf den in einer Vielzahl von Projekten in der chemischen Industrie seit 1989 gewonnenen Erfahrungen. Die bei diesen Anwendungen gemachten Erfahrungen zeigen, dass für den produktiven Einsatz neuronaler Netze in der chemischen Industrie ganz spezifische Anforderungen bestehen, die von NN-Tool vollständig abgedeckt werden. Dies sind insbesondere die folgenden Punkte:
Neben der Software zur Erstellung der Netze stehen darüber hinaus verschiedene Optimierungswerkzeuge zur Auswertung der erstellten Modelle zur Verfügung. Insbesondere lässt sich damit die sogenannte "inverse Fragestellung" beantworten. Das empirische Modell beschreibt zunächst die Abhängigkeit der Ausgangsgrößen (z.B. Qualitätsgrößen) von den Eingangsgrößen (z.B. Rezepturen und Betriebsparameter). D.h. man muss das Modell mit den Rezepturen und Betriebsparametern füttern, dann bekommt man eine Prognose für die Qualitäten. Von besonderem Interesse ist jedoch die folgende Frage: "Wenn ich diese oder jene Qualitäten erreichen will, wie müssen denn dann die Rezepturen und Betriebsparameter sein?" (inverse Fragestellung) Bei dieser Fragestellung treten typischerweise noch Nebenbedingungen auf. So ist es in der Regel der Fall, dass bestimmte Rezepturkomponenten mit gewissen Minimalkonzentrationen in der Rezeptur auf jeden Fall vertreten sein müssen, oder dass die Betriebsparameter in bestimmten Grenzen gehalten werden müssen. Das genannte Optimierungswerkzeug ist in der Lage, unter Berücksichtigung einer Vielzahl von Neben- und Randbedingungen auf der Basis des erstellten Modells optimale Betriebspunkte und Rezepturen zu ermitteln. Weitere Anwendungskomponenten ermöglichen die Anbindung der erstellten Modelle an Prozessleitsysteme für "Softsensoranwendungen" und "modellgestützte Regelungen" (siehe Optimierung). 4.
Zusammenfassung
Künstliche neuronale Netze können als äußerst
leistungsfähige Werkzeuge zur Analyse, Optimierung und Regelung bestehender
Anlagen, Verfahren und Rezepturen angesehen werden. Gerade die Modellierung
der Qualität eines Produkts als Funktion der Betriebsweise bereitet heute
oft noch größte Schwierigkeiten. In diesem Bereich kann das Anwendungsspektrum
neuronaler Netze kaum überschätzt werden. |